Represented while preserving its original size. By connecting the area of a circle to the area of a parallelogram, students can establish meaningful connections to their prior study of area of parallelograms in 6.G.1. The learning map section for this sequence of activities includes prerequisite knowledge of length, perimeter, and the ability to represent and solve equations. Building on an understanding of length, students can learn to explain diameter and radius.
An understanding of perimeter provides the foundation for students to explain circumference. Circumference is really just another way of talking about the perimeter, or the distance around, a circle. This can be calculated in exact form (in terms of \(\pi\) or as a decimal approximation using the circumference formula. From there you can also solve applied problems or more complicated mathematical problems using your general understanding of circles and their properties.
Ask students what the base of the parallelogram would be related to the original circle. Questions could include, "Can you describe where the circumference of the circle falls on the decomposed circle? " and, "If the whole circumference is represented somewhere in this image, what fraction of the circumference falls here ? " Note that as the sectors get smaller, the shape gets closer and closer to a rectangle. Remind students what the formula is for area of a parallelogram, and use this to derive the formula for the area of a circle. An example process is shown following this paragraph.
The circumference of a circle of radius $r$ is $2\pi r$. This well known formula is taken up here from the point of view of similarity. It is important to note in this task that the definition of $\pi$ already involves the circumference of a circle, a particular circle. In order to show that the ratio of circumference to diameter does not depend on the size of the circle, a similarity argument is required. Two different approaches are provided, one using the fact that all circles are similar and a second using similar triangles.
This former approach is simpler but the latter has the advantage of leading into an argument for calculating the area of a circle. The circumference or perimeter of a circle is defined as its boundary or complete arc length. In a circle, all the points lying on the boundary are equidistant and are placed at equal distances from the center. The formula to calculate the circumference is given by the product of π and the diameter of the circle. The formula for the area of a circle is given by 𝜋 r2, where r is the radius of the circle. The value of 𝜋, pronounced pi, is 22/7 or 3.14.
Area Of A Circle Formula Explained Pi is the ratio of the circumference to the diameter of a circle. It is one of the widely used mathematical constants. The area of the circle is measured in terms of square units.
Whatever be the unit of the radius, diameter or circumference, the same will be for the area of the circle but in terms of squares. In this article about the circumference of a circle, we saw the definition, formulas, and ways to find out the circumference of a circle, along with several solved examples. The learning outcome of this article is that one can calculate the circumference of circular objects and circular paths. The first solution requires a general understanding of similarity of shapes while the second requires knowledge of similarity specific to triangles.
When the formula for calculating the circumference of a circle is used, the circle's radius is considered. As a result, the radius or diameter value must be known to calculate the circle's perimeter or circumference. The circumference of any form specifies the route or border that surrounds it in mathematics. In other terms, the circumference is also known as the perimeter, and it is used to determine the length of a shape's contour. Two formulas are used to find circumference, C, depending on the given information.
Both circumference formulas use the irrational number Pi, which is symbolized with the Greek letter, π. Pi is a mathematical constant and it is also the ratio of the circumference of a circle to the diameter. Although the circumference of a circle is the length of its boundary, it cannot be calculated with the help of a ruler like it is usually done for other polygons. This is because a circle is a curved figure. Therefore, to calculate the circumference of a circle, we apply a formula that uses the radius or the diameter of the circle and the value of Pi (π). Is called the circumference and is the linear distance around the edge of a circle.
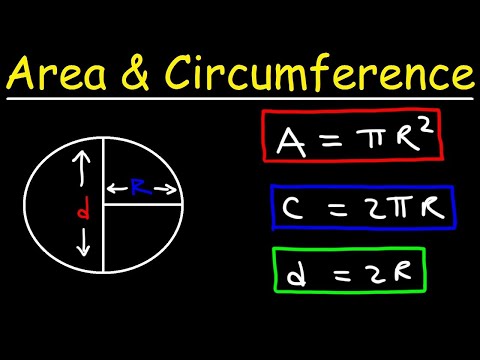
The circumference of a circle is proportional to its diameter, d, and its radius, r, and relates to the famous mathematical constant, pi (π). A circle is a closed shape formed by tracing a point that moves in a plane such that its distance from a given point is constant. The word circle is derived from the Greek word kirkos, meaning hoop or ring.
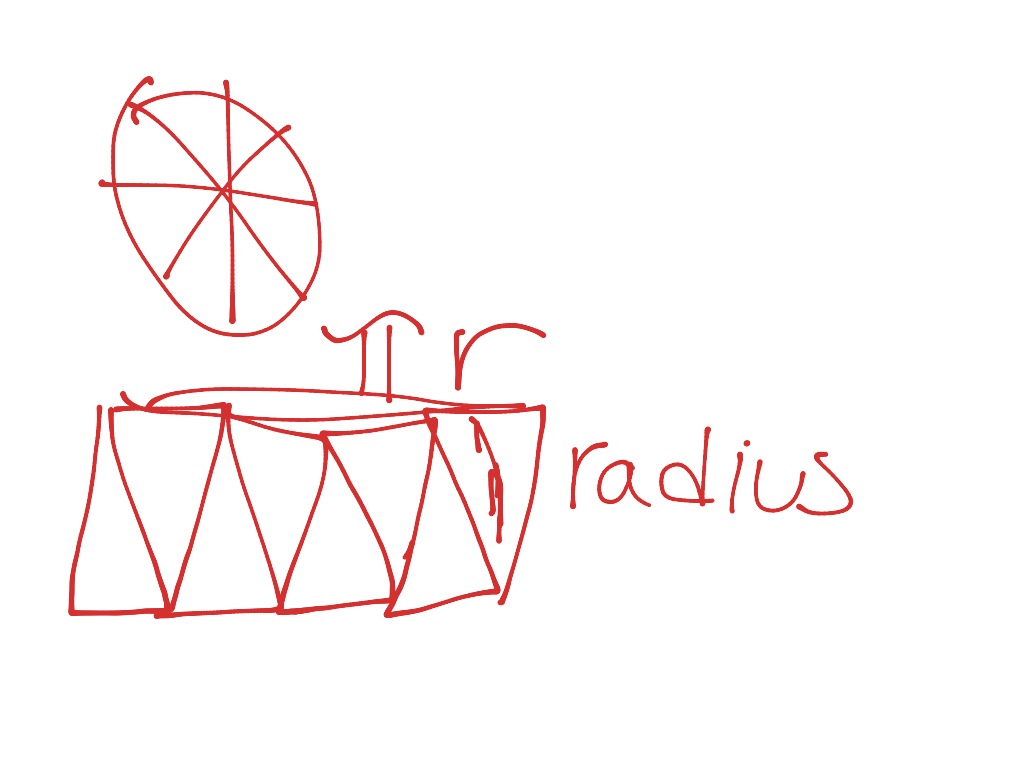
In this article, we cover the important terms related to circles, their properties, and various circle formulas. This first argument is an example of MP7, Look For and Make Use of Structure. The key to this argument is identifying that all circles are similar and then applying the meaning of similarity to the circumference. The second argument exemplifies MP8, Look For and Express Regularity in Repeated Reasoning. Here the key is to compare the circle to a more familiar shape, the triangle. In this method, we divide the circle into 16 equal sectors.
The sectors are arranged in such a way that they form a rectangle. All sectors are similar in area, so hence all sectors' arc length would be equal. The circle's area would be the same as the area of the parallelogram shape or rectangle. The content of the article consists of the definition of a circle its properties and a detailed study of the circumference formula.
The article also contains some solved sample numerical problems related to the circumference formula for reference. Here we have described the formulas to calculate the circumference of a circle in Excel. If you have any other ideas or question, do share with us here in the comments section below.
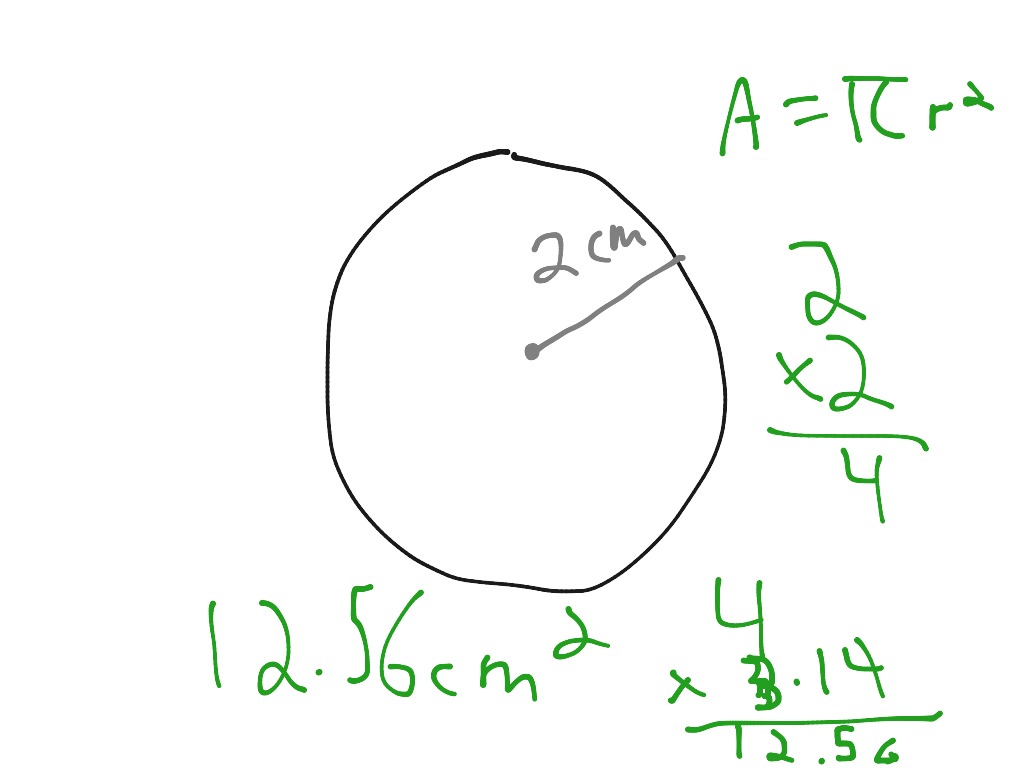
Say you're trying to calculate the area of a circle with a radius of 3 inches. You would multiply 3 times 3 to get 9, and multiply 9 times π. Also note that when you multiply inches by inches, you get square inches, which is a measurement of area instead of length. Students beginning geometry can expect to encounter problem sets that involve calculating the area and circumference of a circle. You can solve these problems as long as you know the circle's radius and can do some simple multiplication. If you learn the value of the constant π and the basic equations for a circle's properties, you can quickly find the area or circumference of any circle.
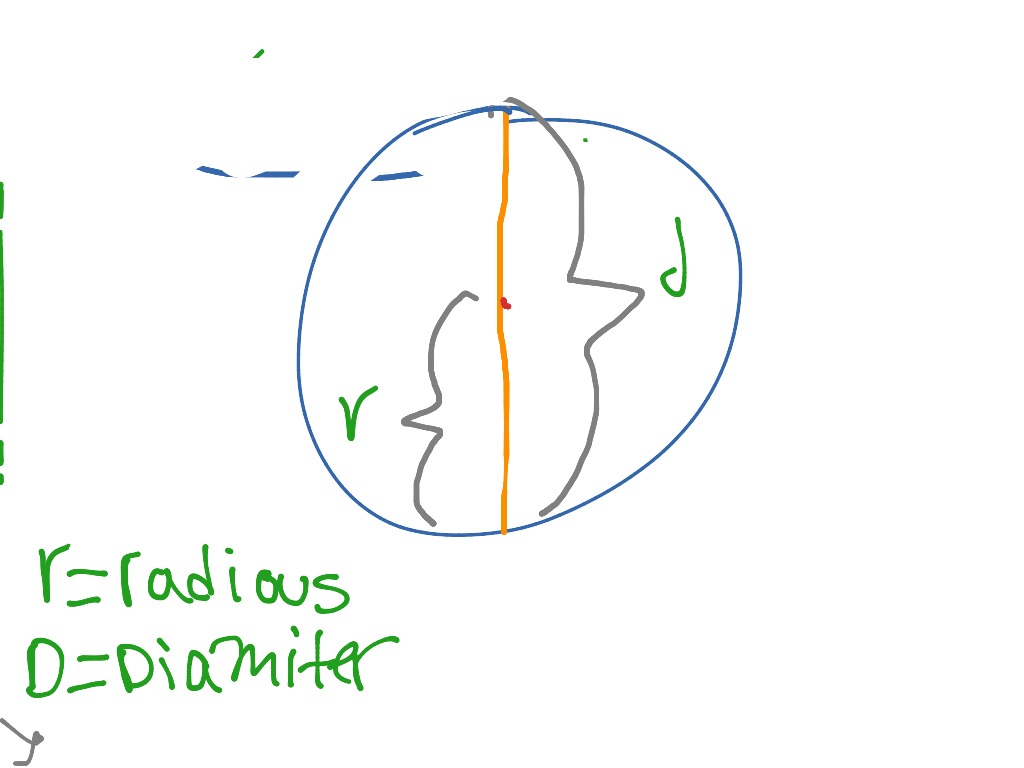
The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle. You can also think of the radius as the distance between the center of the circle and its edge.
The radius of the circle is taken into account when using the formula to determine the circle's circumference. As a result, to calculate the perimeter of a circle, we must first determine the radius or diameter. The mathematical formulas usually come with a set of theorems and proves.
The scientific nature of the subject makes it possible to prove any of the established formulas or theories. Similarly, the formula of the circumference of a circle has been proven. Follow the link where the subject experts have explained in detail and proved that the circumference of a circle is 2πr. This is how we calculate the circumference of a circle and understand its difference from the area.
It is a one-dimensional physical quantity that can be easily understood and calculated if we follow how the formula is determined. Focus on the solved examples and start using the formula to understand the concept better. Ask students what they think would happen if they could cut the circle into an infinite number of sectors and arrange them in a similar fashion . Ask students what they think is true about the area of this figure compared to the area of the original circle . Draw the radius on one of the sectors as shown in the following image . Ask students what measurement this would be, approximately, in a parallelogram .
If students struggle to answer, you could draw in a parallelogram as shown in the following image to scaffold the question. In this image, you can see 16 sectors, including 8 green and 8 blue ones. The green highlighted sectors represent the circle's half circumference while the other half of circumference is represented by blur highlighted ones. By increasing the number of the sectors cut from the circle, the parallelogram will change into a rectangle. The length of the rectangle would b equal to πr with a width equal to r. The upper half of a circle centered at the origin is the graph of the function , where x runs from to .
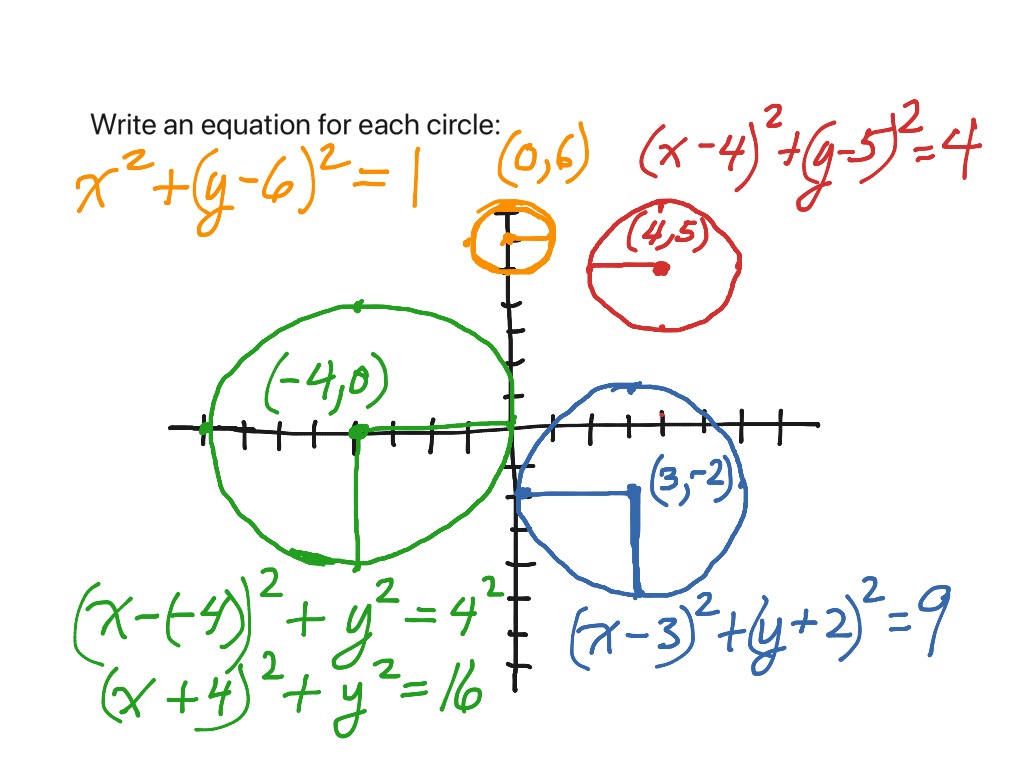
The circumference of the entire circle can be represented as twice the sum of the lengths of the infinitesimal arcs that make up this half circle. This will result in standard form, from which we can read the circle's center and radius. When you are doing calculations involving a circle, you frequently use the number π, or pi. Pi is defined as being equal to the circumference of a circle -- the distance around that circle -- divided by its diameter. However, you don't need to memorize this formula when working with π, since it is a constant. Why is the formula to find the area of a circle 𝜋r²?
To derive the area of a circle formula, divide a circle into various triangles, such that these triangles can be joined in the form of a rectangle as shown in the figure. The more the number of sections, the more clear the rectangle shape will be. Multiply the square root by 2 to find the circumference.
Finally, complete the formula by multiplying the result by 2. This leaves you with a final number, which is the circle's circumference. A circle is divided into congruent sectors . The sectors are pulled out of the circle and are arranged as shown in the middle diagram.
The length across the top is half of the circumference. When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram. As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left. When it comes to circumference, that means understanding that it represents the distance around the circle.
So, if you are given a real-life situation involving finding a distance like this you know to apply the circumference formula. The distance around a polygon, such as a square or a rectangle, is called the perimeter . On the other hand, the distance around a circle is referred to as the circumference . Therefore, the circumference of a circle is the linear distance of an edge of the circle.
Pi is a constant value used for the measurement of the area and circumference of a circle or other circular figures. The symbol of pi is π and its numeric value is equal to 22/7 or 3.14. Further, these numeric values are used based on the context of the equation. The perimeter of a circle is the same as the circumference of a circle. It is the total length of the outer boundary of the circle. The perimeter or circumference of a circle is the product of the constant 'pi' and the diameter of the circle.
It is expressed in linear units like m, inch, cms, feet. We do not call the distance around the outside of a circle, the perimeter. Below you'll find definitions for "circle" vocabulary and the circumference formula.
The perimeter formula is one of the easier formulas to remember in math! The perimeterof a shape is the distance around the outside of the shape. Therefore, all we need to do is add the measurement of each side of the shape and we will have the perimeter. The importance of pi has been recognized for at least 4,000 years. By the start of the 20th century, about 500 digits of pi were known.
With computation advances, thanks to computers, we now know more than the first six billion digits of pi. The base of the figure is represented by half the circumference of the circle, and the height of the figure is represented by the radius of the circle. Therefore, using the formula for the area of a parallelogram, the area of a circle equals half the circumference times the radius. In the above figure, you can see two formulas.
C represents the circle's circumference in the first formula, also denoted as P. The circle circumference is the perimeter of an elliptical or circular shape. In other words, this is the arc length or boundary length of the circle; if we straightened it out or open up in a line segment.
Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference. While most people think that formulas have no practical use, they are critical factors in many everyday life routines. A circle is a closed flat geometrical figure.





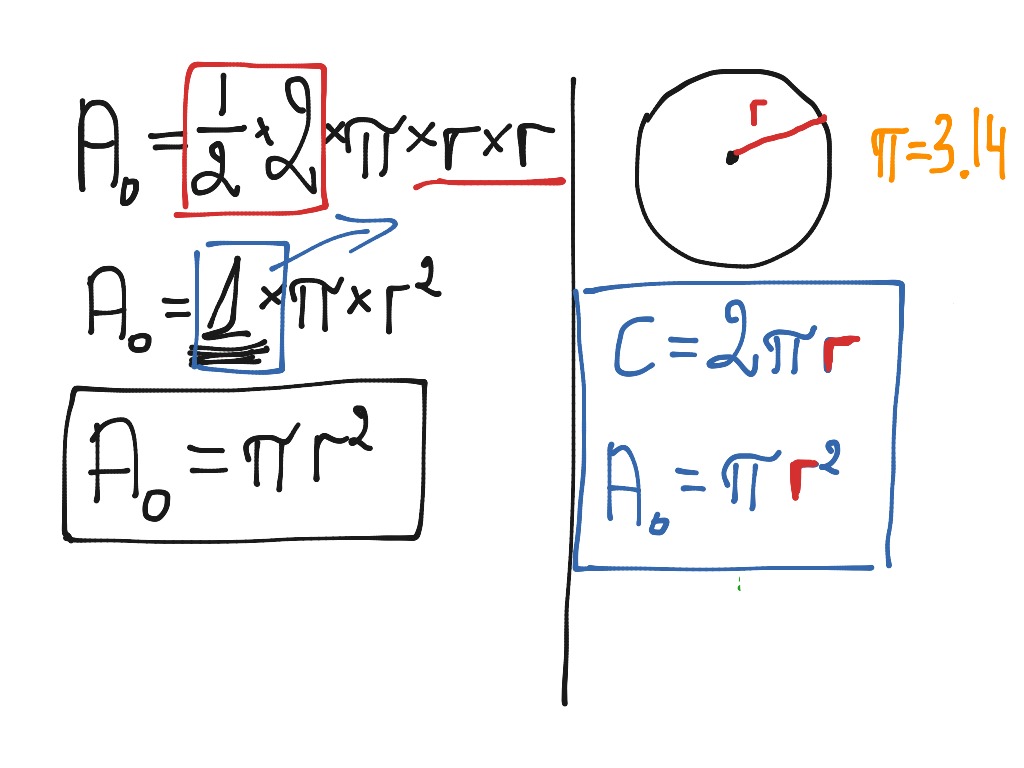





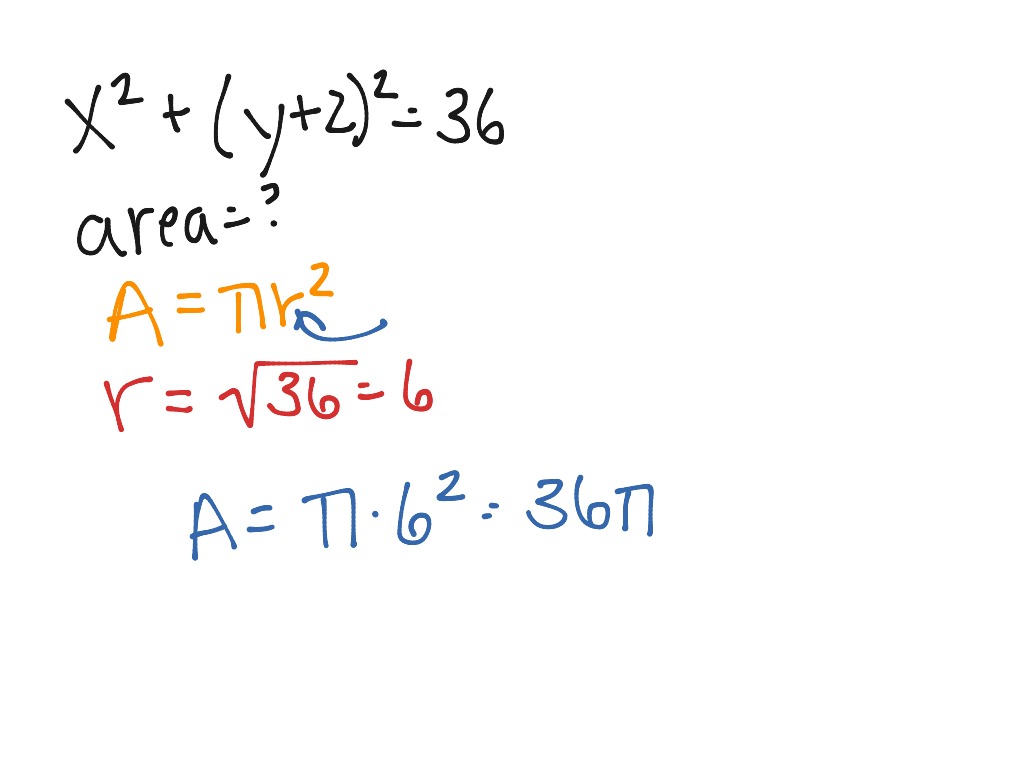
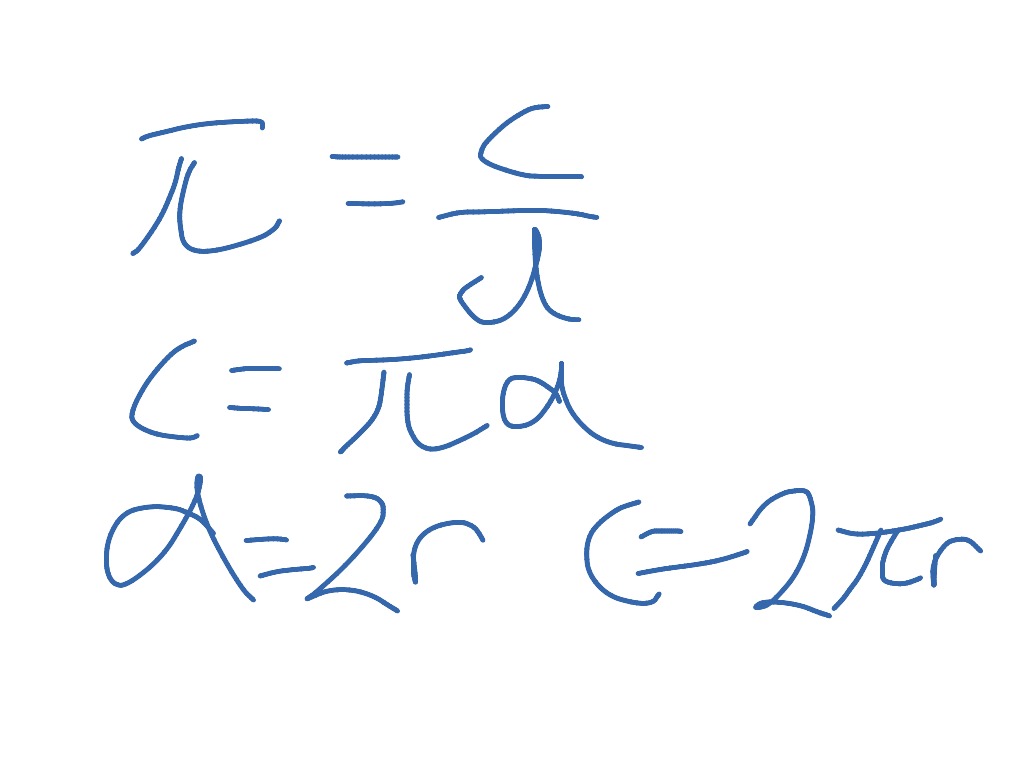


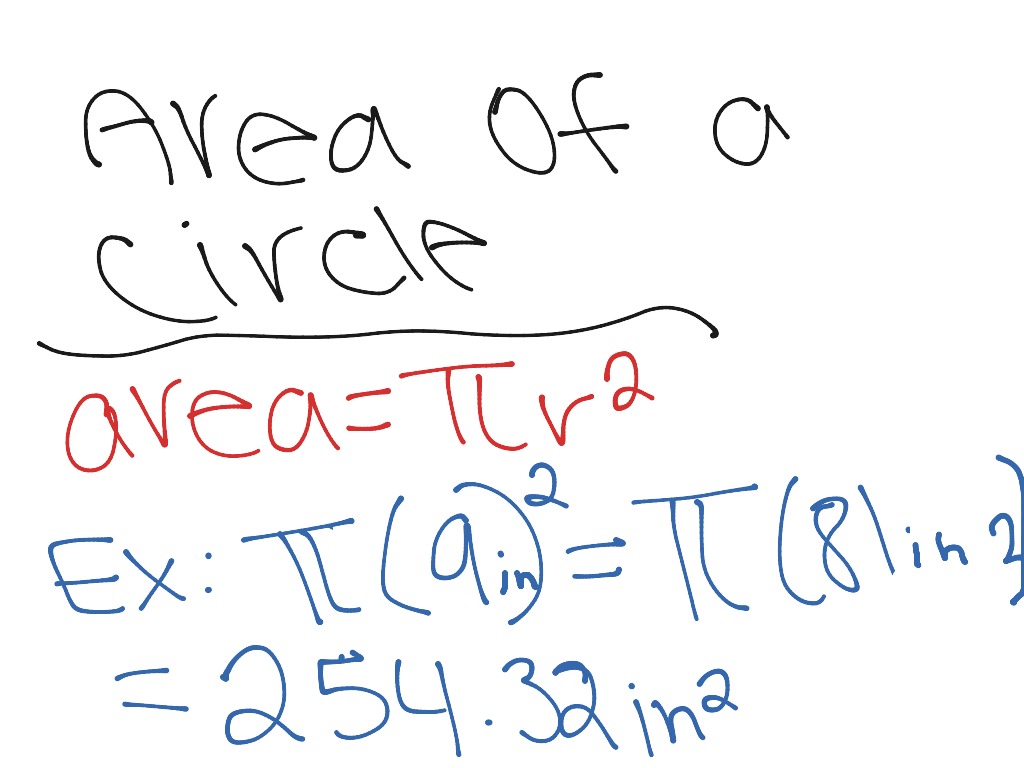







No comments:
Post a Comment
Note: Only a member of this blog may post a comment.